

The Advent of Code is an annual programming challenge which has been running every December since 2015. Which makes the 2024 one the tenth anniversary! Every day a new, two-part puzzle is released, and people all over the world race to collect the stars and save Christmas / help Santa / fix snow production or otherwise rescue the World from calamity. For those of us in Europe this means an early alarm call every morning, for those in western North America it's an evening thing.
The website and the puzzles are deliberately kept in a very low-key, mostly monochrome, text-only format for maximum accessibility. Yet the worlds it describes are varied, dramatic, funny and occasionally vast. Therefore, visualising these problems in different ways is a popular, yet entirely optional extra activity.
Not all of the puzzles lend themselves to useful visualisation, so here I've picked out just a few from the 2023 and 2024 calendars to turn into animations. Perhaps some of the behaviours shown here uncover surprises in the way these things actually change.
In this puzzle, molten lava has been collected from the production facility and needs to be transported to the factory with a minimum amount of heat loss. Wheeled crucibles can transport the lava across the city grid in a frighteningly high number of possible routes, each of which incurring a corresponding heat loss. The problem is to find the best route so that the lava is still as hot as possible when it arrives at the factory.
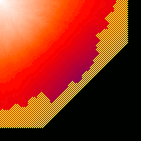 | 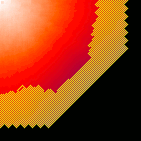 |
|
| Part 1 (click for animation) | Part 2 (click for animation) |
There are certain restrictions on the movement of the crucibles, and these restrictions are different for parts 1 and 2, this is why the exploration front (the squares with yellow highlights) are different for each. Part 1 has (almost) vertical and horizontal fronts, whereas the dynamics of part 2 introduce diagonal fronts.
The exploration continues for some distance inside the main front, and "boils" around in a more complicated way for part 2. Also the final temperatures appear in a more "blocky" way in part 2, especially around the origin in the top-left corner.
How it was made: python and pillow to produce png frames and then combine to a webp.
In this puzzle, an elf is exploring a garden containing scattered rocks. The problem is to find out how many of these square plots the elf can visit after a given number of steps (each one going north, south, east or west, not diagonal).
In part 2, the garden becomes infinite, so the squares which can potentially be explored by the elf expand outwards in all directions, and the number of squares covered expands dramatically.
 |
| Part 2 (click for animation) |
The important point is to find the patterns in this exploration, and here I'm focussing exclusively on the exploration front to the west. With each step, the elf can additionally explore one more square in any direction from each of the previously visited squares (those marked in light blue), as long as it's not occupied by a rock (marked here as grey squares).
I'm scrolling the view here to keep track of the furthest point to the west which can be visited by the elf, but obviously a very similar picture would emerge by tracking the other extremities too.
The surprise for me here was how diagonal and straight the wavefront actually was, I thought it would be much more strongly affected by the rocks and deformed to be non-linear.
The looping animation here also emphasises the regularity of the patterns, as the garden (and its rocks) repeat infinitely in all directions.
How it was made: same as day 17, with python and pillow to produce png frames and then combine to a webp.
This puzzle has another maze to navigate, but with a twist — instead of trying to find the shortest path from the entrance to the exit, this time our protagonist wishes to take a long walk through the forest and this needs to be the longest walk possible in order to enjoy it to its fullest ;)
In part 1 we're not allowed to walk uphill because the slopes are steep and icy, so many of the possible paths are not possible, hence the longest path from top to bottom only covers a fraction of the forest. In part 2 we realise that going uphill is also possible, so the search space increases substantially.
 |  |
|
| Part 1 (click for animation) | Part 2 (click for animation) |
In these animations the forest paths are marked in green, and the optimum route is highlighted in yellow. For part 1 uphill slopes are forbidden, so the network is quite limited, but for part 2 it can take advantage of the uphill slopes as well to produce a much longer route to the exit (over three times as long).
How it was made: python to produce pov files, povray to produce png frames, and then python and pillow to combine to a webp. Calculating the heights of each part of the forest is not completely trivial though, because the heights are only required for the 3d visualisation, not for the solving of the puzzle itself!
My final ranking (for finishing day 25 part 2) is somehow getting worse every year, going over 2000 for the first time since starting in 2021. But I did get 5 days this year on which I finished part 1 in the top 1000, and 3 days on which I finished part 2 in the top 1000, so that's something. Looking at the change in rank from part 1 to part 2, my best day was day 3 where I improved my rank by over 3000, and my worst day was day 24 (swapping the pairs of outputs) where I got really stuck and my second part rank was over 4000 worse than part 1. Importantly, I finished all the days on the day itself, rather than having to sleep on some like last year.
A lot of effort goes into the calendar itself and how it's built up throughout the month. Therefore, here's an animation made up from the gradual reveal, and showing the animations at the end.
 |
| Calendar (click for animation) |
How it was made: the regular screenshot function to save images twice a day from the browser, then gimp to assemble the frames together and line them up (the alignment changed a couple up times during the month). Then recordmydesktop to record the final animation, ffmpeg to extract the frames from the ogv, and then gimp to put the frames together and save as gif.
On this day from 2024, there are 500 robots whizzing around rather quickly in different directions. It's not quite clear why such chaos is necessary, but apparently it's in order to provide "maximum bathroom security". Hmmm.
Anyway, at some point in time, the chaos resolves for a fraction of a second, and the apparently random positions of the robots magically crystallise to form an incredibly brief image. For unknown reasons, this forms a picture and we have to find the time at which this happens.
 |
| Part 2 (click for animation) |
How it was made: same as last year, with python and pillow to produce png frames and then combine to a webp.
Not all of the days lend themselves to animations like this, but maybe there are some from earlier calendars which could also be visualised in similar ways?
If you have any ideas, just let me know.