Kakuros are number puzzles, which are growing in popularity and gradually finding their way into newspapers, magazines and books. Also known as "Cross Sums", they require logic and simple number addition to complete them. Puzzles can vary in difficulty from the very easy to the very fiendish.
Kakuros share some similarities with a regular crossword puzzle (interlocking horizontal and vertical sets of squares, each with a clue), some similarities with Sudokus (each square uses one of the numbers 1 to 9), and slight similarities with Nonograms (clues are numbers, and addition is required).
Each clue consists of a single number, for example 12. The row or column of squares referred to by this clue then has to add up to the given number. So for example if the 12 referred to a row of two squares, one of the squares could be a 5 and the other one a 7. In this case there are several possibilities to add up to 12, and even if you knew from the other clues that it must be a 5 and a 7, you still need to work out whether it's 5 and 7, or 7 and 5.
There is one other rule, to make it easier. Within each clue, you can't have the same number more than once. So for example that clue of 12 couldn't be 6, 6 because that repeats a number. The numbers can appear in other clues though, of course, it's only within a clue that numbers can't be repeated.
So where to start? Clearly we can't get very far with that example of 12, because there are too many possibilities. But we can search around for clues which leave fewer doors open. If you think about the possible permutations, the clues with either very small or very large numbers turn out to be easiest, because there are fewer ways to make them. For example, the clue 3 can only ever be made up from a 1 and a 2. Similarly, a clue of 17 in two squares can only ever be an 8 and a 9. Then you've just got to figure out the order of those numbers.
Some numbers crop up so regularly that they'll quickly become familiar and you can instantly know their combinations. For example, 6 in three squares has to be 1-2-3 (and its permutations of course), and 30 in four squares has to be 6-7-8-9. See the cheat sheet for a quick reference guide.
When two such clues intersect, you can usually tell quite a lot. For example, one popular starting point is a clue of 3 intersecting with a clue of 4, as shown in the diagram to the right:
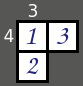As we saw, the 3 must have a 1 and a 2, and similarly the 4 must have a 1 and a 3 (it can't be 2 and 2 because of the "no repeats" rule). So therefore, the square where the 3 and the 4 intersect, must be a 1, and the others can then be filled in straight away.
Another easy starting point is the intersection of a clue 17 (in two squares) and clue 16 (in two squares). In exactly the same way, one of these clues has a 9 and an 8, and the other must have a 9 and a 7. So the intersection can only be the 9, and the rest can be filled in.
You can probably figure out for yourself what happens when the clue 16 (in two squares) meets the clue 14 (in two squares). And likewise when 4 (in two squares) crosses 6 (in two squares).
To help you along, there's a cheat sheet showing the possibilities for various clues and clue lengths. Without listing every possible combination, it does point out the unique solutions which are the most useful. These possibilities can also be used to help solve Killer Sudokus too.
For more information on Kakuro puzzles and how to solve them, have a look at the Wikipedia page, and follow the links there. For other online puzzles see kakurolive.com (English), atksolutions.com (English) or kakuro-world.com (German).